Plantransformasjoner
Translasjon
 |
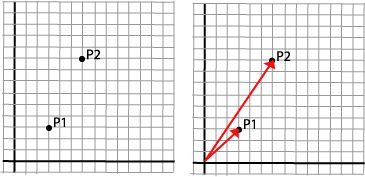
Med translasjon forstår vi å flytte, eller parallellforskyve, en figur. Vi tar utgangspunkt i et enkelt punkt. Dette er en enkel operasjon som er lett å formulere matematisk. Vi vil flytte punktet P1 til en ny posisjon P2. P1=(x1,y1)=(3,3) P2=(x2,y2)=(8,5) |
Vi ser uten videre at
x2=x1+5 y2=y1+2
Translasjon er altså bestemt ved å addere forskyvningen i x-retningen og y-retningen: tx og ty:
x2=x1+tx
y2=y1+ty
Vi tar for gitt at vi kan flytte hele figurer ved å flytte alle enkeltpunktene. For en mangekant, et polygon, betyr dette å flytte alle hjørnene.
Skalering
Vi tar igjen utgangspunkt i et enkelt punkt: P1.
P1=(x1,y1)=(3,3)
Vi "skalerer" punktet ved å multiplisere med en skaleringsfaktor i x-retningen, sx=2, og en i y-retningen, sy=3, og får
P2=(x2,y2)=(6,9)
Sammenhengen er altså:
x2=x1·sx
y2=y1·sy
Nå virker det litt rart å si at vi skalerer et punkt, siden et punkt i geometrisk forstand er uten utstrekning. Det er bedre å si at vi skalerer en vektor.

|
Dersom vi betrakter operasjonen på et polygon, ser vi
at effekten blir litt mer komplisert enn tilfellet var ved translasjon
(parallellforskyvning). I tillegg til at enkeltpunktene flyttes,
endres også vinkler og areal av polygonet.
Merk: Skalering er uttrykt i forhold til origo. |
Rotasjon
 |
Rotasjon er litt mer komplisert å uttrykke og vi må bruke trigonometri for å formulere oss.
P1=(x1,y1)=(r·cos(v1),r·sin(v1))
P2=(x2,y2)=(r·cos(v1+v2),r·sin(v1+v2))
|
Vi introduserer de trigonometriske formlene for summen av to vinkler:
sin (a+b) = cos(a)·sin(b)+sin(a)·cos(b)
cos (a+b) = cos(a)·cos(b)-sin(a)·sin(b)
og får:
P1=((r·cos(v1), r·sin(v1) ) P2=(r·cos(v1)·cos(v2)-r·sin(v1)·sin(v2), r·cos(v1)·sin(v2)+r·sin(v1)·cos(v2))
Vi setter inn:
x1=r·cos(v1) y1=r·sin(v1)
i P2s koordinater:
P2=(x2,y2)=(x1·cos(v2)-y1·sin(v2),
x1·sin(v2)+y1·cos(v2))
og vi har uttrykt P2s koordinater ved hjelp av P1s koordinater og rotasjonsvinkelen v.
x2= x1·cos(v)-y1·sin(v) y2= x1·sin(v)+y1·cos(v)
Merk: Rotasjon er uttrykt om origo. Det betyr også at sidene i figurer som roteres også danner nye vinkler med aksene etter rotasjonen. Vi regner positiv rotasjonsvinkel mot klokka.
Matriser
Vi sitter altså igjen med følgende ligningssett som beskriver de tre basisoperasjonene:
| Translasjon bestemt ved tx og ty |
x2=x1+tx y2=y1+ty |
| Skalering bestemt ved sx og sy |
x2=sx·x1 y2=sy·y1 |
| Rotasjon bestemt ved v |
x2= x1·cos(v)-y1·sin(v) y2= x1·sin(v)+y1·cos(v) |
Vi ønsker å finne en felles form for representasjon av disse operasjonene. Vi vet fra lineær algebra at vi kan representere slike lineære sammenhenger ved matriser.
Tar vi ligningssettene direkte får vi:
|
Translasjon bestemt ved tx og ty |
|x2| |x1| |tx| | | = | | + | | |y2| |y1| |tx| |
|
Skalering bestemt ved sx og sy |
|x2| |sx 0| |x1| | | = | | * | | |y2| |0 sy| |y1| |
|
Rotasjon bestemt ved v |
|x2| |cos(v) -sin(v)| |x1| | | = | | * | | |y2| |sin(v) cos(v)| |y1| |
De aktuelle matriseoperasjonene, multiplikasjon og addisjon, er beskrevet i modulen: Algebra.
Homogene koordinater
Vi har altså litt forskjellige former for de tre basisoperasjonene. Vi ønsker samme form og introduserer homogene koordinater. Det vil si at vi skriver en posisjonsvektor slik:
| x | | y | | 1 |
Da kan vi skrive alle basisoperasjonene som multiplikasjon mellom en 3 x 3 matrise og en 1 x 3 vektor.
| Translasjon |
| x2 | |1 0 tx| |x1| | y2 | = |0 1 ty|*|y1| | 1 | |0 0 1| |1 | |
| Skalering |
| x2 | |sx 0 0| |x1| | y2 | = |0 sy 0|*|y1| | 1 | |0 0 1| |1 | |
| Rotasjon |
| x2 | |cos(v) -sin(v) 0| |x1| | y2 | = |sin(v) cos(v) 0|*|y1| | 1 | |0 0 1| |1 | |
Vi har en generell form
P2=M·P1
der P1 og P2 er uttrykt i homogene koordinater. Den tredje koordinaten, 1-tallet, trenger vi ikke bekymre oss. Vi forsøker ikke å gi noen geometrisk forklaring av denne. Hele vitsen med homogene koordinater er å standardisere matematikken i transformasjonene. Den tredje koordinaten forblir uforandret ved de grunnleggende transformasjonene og, som vi skal se senere, ved kombinasjoner av dem. Modulen Homogenisering drøfter temaet litt nærmere.
Geometri
Vi skal dra nytte av denne felles uttrykksformen til mange ting. La oss først se på noe enkle sammenhenger mellom matriser og geometri.
Identitetsmatrisen
En viktig matrise er identitetsmatrisen:
| 1 0 0 | I=| 0 1 0 | | 0 0 1 |
Den transformerer et punkt til seg selv: P1=P2=I·P1
Dette kan vi tolke som
- translasjon med (0,0)
- rotasjon med 0 grader, siden cos (0)=1 og sin (0) =0
- skalering med (1,1)
Vi vil få bruk for identitetsmatrisen i mange situasjoner. I OpenGL er det en egen funksjon for å spesifisere denne som gjeldende transformasjonsmatrise:
glLoadIdentity()
Vi skal senere se hvorfor denne funksjonen er viktig.
Speiling
Vi kan speile et punkt om koordinataksene med matriser:

|
Om y-aksen, en skalering med (-1,0):
| -1 0 0 | SY=| 0 1 0 | | 0 0 1 |Om x-aksen, en skalering med (0,-1): | 1 0 0 | SX=| 0 -1 0 | | 0 0 1 | |
Shearing
En spesiell operasjon som kalles shearing er en skalering langs
den ene aksen som er avhengig av koordinaten på den andre
aksen, f.eks. x-aksen avhengig av y:

|
| 1 s 0 | S=| 0 1 0 | | 0 0 1 | Dette er en framstilling av x2=x1+s·y
og y2=y1. Figuren
viser en slik shearing anvendt på et rektangel og med s=1. |
Projeksjon
Vi kan projisere et punkt, f.eks. ned på x-aksen ved matrisen
| 1 0 0 | I=| 0 0 0 | | 0 0 1 |
I planet ser vi at en slik parallellprojeksjon ikke har annen effekt enn å fjerne y-koordinaten. Konsekvensen av dette vil alltid bli en linje langs x-aksen. I rommet blir projeksjoner litt annerledes, og mer interessant.
Sammensatte operasjoner
Det er vel og bra at vi har en felles form for basistransformasjonene. Gevinsten skal vi ta ut ved å se hvordan vi kan kombinere geometriske operasjoner ved å kombinere matriser.
Vi kan kombinere flere geometriske operasjoner ved å multiplisere de respektive matrisene. Før vi går løs på dette, kan vi se litt på gevinstene. De er i hovedsak tre:
- Framstillingshastighet. Vi vil typisk ha en situasjon der vi må beregne koordinater for et stort antall punkter, kanskje tusenvis, når tegningen vår skal framstilles på skjermen. Disse punktenes koordinater endres av forskjellige årsaker og deres posisjon kan være resultatet av et stort antall geometriske transformasjoner. Vi ønsker å redusere antall regneoperasjoner for hvert punkt. I stedet for å multiplisere hver vektor (punkt) med alle matrisene som er involvert etter tur, ønsker vi å kunne multiplisere med kun en matrise. I OpenGL er det slik: Det er til en hver tid en modellmatrise som gjelder og som alle punkter alltid multipliseres med.
- Modellering. Dette vil vi komme tilbake til senere. Men la oss foreløpig antyde problemet med å si at vi ofte har figurer som er sammensatt av ulike komponenter. De ulike komponentene er kombinert slik at deres posisjon er avhengig av andre deler av figuren. F.eks. er fingrene på en robot avhengig av posisjonen til den armen de sitter på armene. Det kan da være lurt å kunne gjenbruke transformasjonsmatriser flere ganger. En praktisk måte å gjøre dette på er å ha en stakk av transformasjonsmatriser. Slik er det i OpenGL.
- Vi kan integrere synstransformasjonen med modelltransformasjonen, se modulen: Modell til skjerm.
La oss se på noen enkle eksempler som illustrerer selve prinsippet.
To translasjoner
Vi begynner med et enkelt eksempel. La oss anta at vi skal gjennomføre to translasjoner på et punkt. La oss anta at den første translasjonen er (2,3) og at den andre er (4,6). Vi kan selvsagt lett ut fra rene geometriske betraktninger fastslå at resultatet bør være en translasjon (6,9). Hvis ikke, må det være noe galt med resonnementet vårt.
De to matrisene er altså:
| 1 0 2 | | 1 0 4 | T1=| 0 1 3 | og T2=| 0 1 6 | | 0 0 1 | | 0 0 1 |
og produktet:
| 1 0 6 | T1*T2=| 0 1 9 | | 0 0 1 |
Vi ser uten videre at resultatet er som ønsket. Vi oppnår en matrise som realiserer den sammensatte operasjonen ved å multiplisere de to enkeltmatrisene. Vi ser også at i dette spesielle tilfellet kunne vi få fram den samlede matrisa ved å addere de to matrisene, men det er spesielt for to translasjoner.
Vi ser også at i dette tilfellet T1·T2=T2·T1. Geometrisk er ikke dette overraskende. Det må bli det samme i hvilken rekkefølge vi utfører translasjonene. Det er imidlertid ikke slik at matrisemultiplikasjon generelt er uavhengig av faktorenes orden. Det vi har her er et spesialtilfelle. Vi vil undersøke sammenhengen mellom rekkefølge og matrisemultiplikasjon nærmere i neste eksempel.
Rotasjon om et annet punkt enn origo
Vi betrakter en trekant med hjørnene a (1,1), b (2,-1) og c (4,2).

Vi ønsker å rotere denne trekanten 90 grader om sitt ene hjørne, a. Vi vet at rotasjon slik vi har beskrevet den ovenfor alltid foregår om origo. Vi må legge en strategi ved å kombinere flere transformasjoner. Vi prøver ut to strategier og forsøker å trekke noen konklusjoner etterpå.
En strategi kan være:
- Flytt origo til rotasjonshjørnet
- Roter 90 grader
- Flytt origo tilbake
Vi kan lett sette opp de tre matrisene som realiserer de tre enkeltoperasjonene:
| Flytt origo til hjørnet a: |
| 1 0 1 | T1=| 0 1 1 | | 0 0 1 | |
| Roter 90 grader: |
| 0 -1 0 | R =| 1 0 0 | | 0 0 1 | |
| Flytt origo tilbake: |
| 1 0 -1 |
T2 =| 0 1 -1 |
| 0 0 1 |
|
Hvis vi følger resonnementet vårt vil vi få en samlematrise M=T1·R·T2, og vi skulle få den ønskede effekten ved å multiplisere alle punktene i trekanten med denne matrisa, P2=M·P1.
| 1 0 1 | | 0 -1 0 | | 1 0 -1 |
M = | 0 1 1 |*| 1 0 0 |*| 0 1 -1 |
| 0 0 1 | | 0 0 1 | | 0 0 1 |
| 0 -1 1 | | 1 0 -1 |
= | 1 0 1 |*| 0 1 -1 |
| 0 0 1 | | 0 0 1 |
| 0 -1 2 |
= | 1 0 0 |
| 0 0 1 |
Vi anvender M på de tre punktene i trekanten og får:
| 0 -1 2 | | 1 | | 1 |
a' = M*a | 1 0 0 |*| 1 |=| 1 |
| 0 0 1 | | 1 | | 1 |
| 0 -1 2 | | 2 | | 3 |
b' = M*b | 1 0 0 |*| -1 |=| 2 |
| 0 0 1 | | 1 | | 1 |
| 0 -1 2 | | 4 | | 0 |
c' = M*c | 1 0 0 |*| 2 |=| 4 |
| 0 0 1 | | 1 | | 1 |
og vi kan tegne resultatet:

Hvilket var det vi ønsket. Strategien vår var altså vellykket.
En alternativ strategi kunne være som følger:
- Flytt trekanten slik at a havner i origo
- Roter 90 grader
- Flytt trekanten tilbake, slik at a havner på sitt opprinnelige
Siden det å flytte punktet a til origo er det motsatte av
å flytte origo til a, så blir den førte operasjonen det samme som det
vi ovenfor har kalt T2. På samme måte blir steg 3, å flytte
trekanten tilbake, det samme som det vi ovenfor har kalt T1.
Den alternative strategien blir da: M=T2·R·T1
.
Hvis vi regner oss gjennom dette får vi:
| 0 -1 -2 |
M = | 1 0 0 |
| 0 0 1 |
Anvender vi denne matrise på trekantens tre punkter får vi en slik løsning: hvilket ikke overraskende er noe annet enn det vi ønsket.
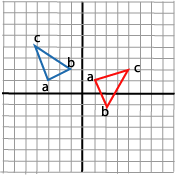
Vi fant ovenfor ut at å flytte punktet til origo og å flytte origo til punktet er motsatte transformasjoner. De samme transformasjonsmatrisene inngår i begge strategiene, men rekkefølgen de anvendes på er forskjellig. Vi så videre at den første strategien med å flytte origo var vellykket. Dette kan lede oss fram til følgende formulering av en strategi for å kople matriser til geometriske resonnementer.
Vi kan gjøre ett av to:
- Vi kan utføre resonnementet på origo og sette opp matrisene i samme rekkefølge som vi resonnerer
- Vi kan utføre resonnementet på figuren og sette opp matrisene i motsatt rekkefølge av det geometriske resonnementet.
Normalt vil vi bruke strategi 1, men av og til kan det være klarere å resonnere etter strategi 2.
I OpenGL
For å forstå hvordan OpenGLs transformasjoner fungerer må vi kikke nærmere på begrepet aktuell transformasjonsmatrise. Det betyr at OpenGL alltid multipliserer koordinatverdier i tegnekommandoer med den aktuelle matrisa før de prosesseres videre og tilslutt, etter enda flere transformasjoner, havner på skjermen. Den grunnleggende tegnkommandoen i OpenGL, for henholdsvis planet og rommet:
glVertex2(x,y) glVertex3(x,y,z)
angir rett og slett hvilken posisjonsvektor som inngår, denne multipliseres med den aktuelle transformasjonsmatrisa, før den prosesseres videre på sin vei mot skjermen. glVertex er i prinsipp det eneste grunnleggende tegneprimitivet i OpenGL.
Den enkleste matrisa er identitetsmatrisa, I. Den foretar seg som kjent ikke noe med koordinatene. Den settes som aktuell transformasjonsmatrise ved
glLoadIdentity()
OpenGL har tre grunnleggende funksjoner som bygger opp den aktuelle transformasjonsmatrisen, i tillegg til glLoadIdentity():
glTranslate() glRotate() glScale()
Når vi kaller en av disse påvirkes den aktuelle transformasjonsmatrisen ved at den nye transformasjonsmatrisen multipliseres til.
Eksempelet med rotasjon om et annet punkt enn origo, kan realiseres slik i OpenGL:
|
Geometrisk operasjon |
OpenGL-kall | Aktuell matrise M |
|---|---|---|
| Nullstill transformasjonene | glLoadIdentity() | M=I |
| Transler origo til a | gltranslate(1,1,0) | M =I·T1 |
| Roter | glRotate(90,0,0,1) | M= I·T1·R |
| Transler origo tilbake | gltranslate(-1,-1,0) | M= I·T1·R·T2 |
Matrisestakken
OpenGL tilbyr en stakk (last-in-first-out-queue) av transformasjonsmatriser, og vi kan pushe matriser til denne stakken og vi kan poppe fra stakken når vi måtte ønske det.
glPushMatrix() glPopMatrix()
På denne måten kan vi ta vare på midlertidige matriser (push) og finne dem fram (pop) etter at vi har brukt andre operasjoner i mellomtiden. Dette er en svært nyttig strategi ved uttegning av ikke-trivielle figurer i OpenGL (og alle andre grafiske pakker). Vi skal komme tilbake til dette flere ganger i programeksempler, men vi kan antyde anvendelsen ved hjelp av et eksempel.
La oss se på en robotarm, med overarm, underarm og tre fingre:
 |
<tegn A> glRotate() <tegn B> glPushMatrix() glRotate() <tegn F1> glPopMatrix() glPushMatrix() glRotate() <tegn F2> glPopMatrix() glPushMatrix() glRotate() <tegn F3> |
Rader og kolonner
I resonnementet så langt har vi beskrevet et punkt med en kolonnevektor, og vi har skrevet P2=M·P1.
Alternativt kan vi beskrive et punkt med en radvektor og skrive P2=P1·M
Vi kan da skrive de tre basisoperasjonene som:
| Translasjon |
| 1 0 0 |
|x',y',z'|=|x,y,z|*| 0 1 0 |
| tx ty 1 |
|
| Skalering |
| sx 0 0 |
|x',y',z'|=|x,y,z|*| 0 sy 0 |
| 0 0 1 |
|
| Rotasjon |
| cos(v) sin(v) 0 |
|x',y',z'|=|x,y,z|*| -sin(v) cos(v) 0 |
| 0 0 1 |
|
Det kan være en nyttig øvelse og regne gjennom konsekvensene av denne formen i tilsvarende eksempler som det vi har arbeidet med ovenfor. En god del grafisk litteratur beskriver transformasjoner på denne måte. Se også transponering av matriser i modulen: Algebra.


