NURB'er
Uniform Non Rational B_splines
Vi tar utgangspunkt i en situasjon som vi kan karakterisere som Uniform Non Rational B_splines. Vi kan illustrere en slik spline slik:
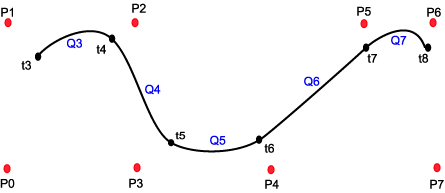
Vi har m+1=8 kontrollpunkter, og m-2=5 kurvesegmenter. Kurven kan beskrives ved en parameter som løper fra t3 til t8. Et kurvesegment er avgrenset av et t-steg. Kurven Qi beskrives når t løper fra ti til ti+1.
Segmentene er koplet slik:
- Q3 er avhengig av P0 ,P1 ,P2 ,P3
- Q4 er avhengig av P1 ,P2 ,P3 ,P4
- Q5 er avhengig av P2 ,P3 ,P4 ,P5
- ...
- Qi er avhengig av Pi-3 ,Pi-2 ,Pi-1 ,Pi
Hver kurve er bestemt av 4 kontrollpunkter. Det betyr at vi har lokal kontroll i den forstand at andre punkter enn de 4 ikke påvirker et kurvesegment. Tilsvarende er hvert kontrollpunkt involvert i 4 kurvesegmenter.
Vi ser at dette er interessant i forhold til det vi kan oppnå med Bezier-kurver. Dersom vi skal ha en sammenhengende Bezier-kurve med så mange kontrollpunkter, vil vi måtte øke graden av kurven til m-1 og vi vil ha en situasjon der alle kontrollpunkter påvirker hele kurven. Dersom vi lager en kurve bestående av kubiske Beziersegmenter vil vi ha lokal kontroll over segmentene, men vi vil miste kontrollen over kontinuiteten i skjøtene når vi endrer enkeltpunkter.
Vi skal se litt nærmere på de enkelte segmentene. Vi kjenner fra modulene Bezier og Polynomer den generelle formen for en slik kurve, eller kurvesegment:
Q(t)=T·M·G,
der T er en radvektor som beskriver kurvens grad, M er en 4x4 matrise som er spesiell for kurveformen og G er en kolonnevektor som beskriver de geometriske føringene.
For kurvesegment nr i kan vi skrive:

Det er to ting å merke seg her.
For det første har vi ikke begrunnet selve matrisen MBS.
For det andre har vi en T vektor som er litt mer komplisert enn det vi kjenner fra Hermit og Bezier, siden vi har (t-ti) i stedet for t. Vi kan uten tap av generalitet erstatte (t-ti) med t, og på den måten få samme T·M for alle kurvesegmentene. Vi vet fra tidligere at dette produktet gir oss 4 vektfunksjoner som, i sin tur forteller oss hvor mye innflytelse hvert av de fire kontrollpunktene har på kurven når t løper fra 0 til 1. For B-Splines blir vektfunksjonene slik.

|
Vi-3 = 1/6(-t3+3t2-3t+1)
Vi-2 = 1/6(3t3-6t2+4)
Vi-1 = 1/6(-3t3+3t2+3t+1)
Vi = 1/6(t3)
|
Der vi altså bruker disse slik:
Qi(t)=Vi-3·Pi-3 +
Vi-2·Pi-2 +
Vi-1·Pi-1 +
Vi·Pi
Så langt har vi etablert og beskrevet komplett en kurveform som er uniform. I det legger vi at alle kurvesegmentene er formulert på samme måte. t-verdiene i kurven ligger like langt fra hverandre: ti+1 - ti = 1
Non Uniform Rational B-splines
I motsetning til det vi har sett på ovenfor skal altså disse kurvene være Rational og Non Uniform.
At de er "Rational" har sammenheng med at kurvene kan beskrives i et homogent koordinatsystem og det har som konsekvens at de kan utsettes for de vanlige transformasjonene uten å endre form. Vi forfølger ikke dette her.
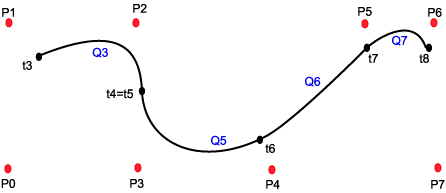
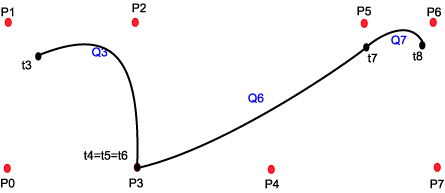
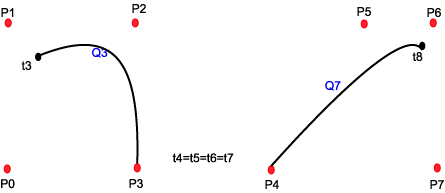
At de er "Non Uniform" betyr at de enkelte segmentene i kurven ikke har samme form, og det betyr at vi kan manipulere kurvens utseende, spesielt kontinuitetsgraden mellom segmenter, ved å manipulere t-verdiene. Det er dette som gjør NURB'er til et hendig modelleringsverktøy. t-punktene, eller overgangene mellom segmentene, kaller vi knuter (eng.:knots). Spesielt ser vi ut fra den beskrivelsen som er gitt ovenfor at dersom vi slår sammen t-verdier så kan vi eliminere kurvesegmenter. Det betyr at nabosegmentene på begge sider henger sammen, men overgangen blir ikke så glatt som i en "uniform" kurve. Slår vi sammen 4 knuter (eliminerer 4 segmenter) så har vi introdusert en diskontinuitet i kurven. Naboene på begge sider har ikke lenger noen felles kontrollpunkter.
De 4 kommenterte figurene nedenfor beskriver noen av disse mulighetene. Merk at disse figurene er håndtegnet, ikke beregnet, og at det derfor kan være unøyaktigheter. Det viktige er å få fram prinsippene.

I openGL
Kurve
// make a nurb object
theNurb=gluNewNurbsRenderer();
expectedError=GLU_INVALID_ENUM;
// draw nurb,using the nurbobject:theNurb
gluNurbsProperty(theNurb,GLU_SAMPLING_TOLERANCE,25.0);
gluNurbsProperty(theNurb,GLU_DISPLAY_MODE,GLU_FILL);
// defining a callback for errorreport
gluNurbsCallback(theNurb,GLU_ERROR,
(GLvoid(__stdcall *)())errorInNurb);
glLineWidth(4.0);
glDisable(GL_LIGHTING);
glColor3f(0.0,0.0,1.0);
// displaying
gluBeginCurve(theNurb);
gluNurbsCurve(
theNurb,
uk_count, // knot count along u
u_knots, // .. and the knots
3, // from one u to the next
& ctpnts[0][0], // the pointarray
4, // order of polynomial, cubic+1
GL_MAP1_VERTEX_3
);
gluEndCurve(theNurb);
gluDeleteNurbsRenderer(theNurb);
Flate
// make a nurb object
theNurb=gluNewNurbsRenderer();
expectedError=GLU_INVALID_ENUM;
// draw nurb,using the nurbobject:theNurb
gluNurbsProperty(theNurb,GLU_SAMPLING_TOLERANCE,25.0);
gluNurbsProperty(theNurb,GLU_DISPLAY_MODE,GL_FILL);
// defining a callback for errorreport
gluNurbsCallback(theNurb,GLU_ERROR,
(GLvoid(__stdcall *)())errorInNurb);
// displaying
gluBeginSurface(theNurb);
gluNurbsSurface(
theNurb,
uk_count, // knot count along u
u_knots, // .. and the knots
vk_count, // knot count along v
v_knots, // .. and the knots
VMAX*3, // from one u to the next
3, // from one v to the next
& ctpnts[0][0][0],
4, // order of polynomial, cubic+1
4, // order of polynomial, cubic+1
GL_MAP2_VERTEX_3
);
gluEndSurface(theNurb);
gluDeleteNurbsRenderer(theNurb);
Trimming
OpenGL gir mulighet for å trimme en NURB-flate. Det vil si at vi kan avgrense deler av flaten vi vil ha med i tegningen og vi kan skjære bort deler av flaten vi ikke vil ha med. Dette gjøres ved å spesifisere lukkede polygoner ved å angi 2D-punkter i parameterområdet. Logikken er slik at de deler av flaten som ligger til venstre for polygonet blir med mens det som ligger til høyre fjernes. Det er derfor viktig at vi spesifiserer punktene i disse trimmepolygonene i riktig rekkefølge. Vi tar med ved å oppgi punktene mot klokka og vi skjærer vekk ved å oppgi punktene med klokka.
Merk at koordinatene til punktene i trimmepolygonene oppgis innenfor kurvens parameterområde, altså de t-verdiene vi opererer med. De faktiske koordinatene til kontrollpunktene er irrelevante i denne opersjonen.
// make a nurb object
theNurb=gluNewNurbsRenderer();
expectedError=GLU_INVALID_ENUM;
// draw nurb,using the nurbobject:theNurb
gluNurbsProperty(theNurb,GLU_SAMPLING_TOLERANCE,25.0);
gluNurbsProperty(theNurb,GLU_DISPLAY_MODE,GL_FILL);
// defining a callback for errorreport
gluNurbsCallback(theNurb,GLU_ERROR,
(GLvoid(__stdcall *)())errorInNurb);
// displaying
gluBeginSurface(theNurb);
gluNurbsSurface(
theNurb,
uk_count, // knot count along u
u_knots, // .. and the knots
vk_count, // knot count along v
v_knots, // .. and the knots
VMAX*3, // from one u to the next
3, // from one v to the next
& ctpnts[0][0][0],
4, // order of polynomial, cubic+1
4, // order of polynomial, cubic+1
GL_MAP2_VERTEX_3
);
// Trimming
// what we want
gluBeginTrim(theNurb);
gluPwlCurve(theNurb,5,& trim_outside[0][0],2,GLU_MAP1_TRIM_2);
gluEndTrim(theNurb);
// what we dont want
gluBeginTrim(theNurb);
gluPwlCurve(theNurb,5,& trim_inside[0][0],2,GLU_MAP1_TRIM_2);
gluEndTrim(theNurb);
gluEndSurface(theNurb);
gluDeleteNurbsRenderer(theNurb);


