Labyrinten
Platen

Figur 1: Her ser man de
små firkantene
som danner selve platen
Det første man kan gjøre er å tegne opp en plate på skjermen som kula skal ligge oppå. Siden man skal kunne ha hull i denne platen, så kan man ikke tegne opp en stor flate for så å tegne hull i den etterpå. Det jeg gjorde var å bygge opp denne flaten av et gitt antall mindre firkanter. Der man da skal ha hull kan man velge å tegne noe annet i stedet for en liten flate. Når man da skal ha en tekstur på denne flaten, så må man trikse litt med tekstur-koordinater for å få det til å se bra ut. Mer om dette senere.
Størrelsen på brettet og størrelsen på de platene er definert som følger:
#define BOARD_WIDTH 20
#define SQUARE_SIZE 0.075
For å tegne opp 20x20 slike små firkanter så kan man gjøre følgende:
- Flytt origo til det innerste venstre hjørnet av hele platen
- La en løkke gå fra 0 til 20(z)
- Ha enda en løkke inne i den første som også går fra 0 til 20(x)
- I den innerste løkka gjør følgende:
- Push matrise stacken
- Flytt origo z * SQUARE_SIZE i positiv retning på z-aksen og x * SQUARE_SIZE i positiv retning på x-aksen
- Tegn opp en firkant
- Pop matrise stacken
Følgende kode vil gjøre susen:
int z,x;
glTranslatef(-BOARD_WIDTH * SQUARE_SIZE / 2, 0.0, -BOARD_WIDTH * SQUARE_SIZE / 2);
for(z = 0;z < BOARD_WIDTH;z++){
for(x = 0;x < BOARD_WIDTH;x++){
glPushMatrix();
glTranslatef(x * SQUARE_SIZE, 0.0, z * SQUARE_SIZE);
glBegin(GL_QUADS);
glNormal3f(0.0, 1.0, 0.0);
glVertex3f(0.0, 0.0, 0.0);
glVertex3f(SQUARE_SIZE, 0.0, 0.0);
glVertex3f(SQUARE_SIZE, 0.0, SQUARE_SIZE);
glVertex3f(0.0, 0.0, SQUARE_SIZE);
glEnd();
glPopMatrix();
}
}
Platen vil derfor tegnes opp fra det bakerste venstre hjørnet mot høyre, en rad av gangen. Hvis vi nå ser på Figur 1, så kan vi se hele platen bygd opp av små firkanter.
 Figur 2: Platen med vegger |
 Figur 3: Platen med vegger |
 Figur 4: Platen og veggene med materiale |
Når man nå har overflaten til platen vår, så kan man tegne "veggene" på den slik at den ser litt mer ut som en plate, og ikke bare et tynt ark. Dette kan gjøres på følgende måte:
- Flytt origo til det ytterste venstre hjørnet av platen
- La en løkke gå fra 0 til 4 og for hver gang løkken kjører, gjør følgende:
- Tegn en vegg
- Flytt origo BOARD_WIDTH * SQUARE_SIZE i negativ retning på z-aksen(innover i skjermen)
- Roter negative 90 grader om y-aksen for så å kunne tegne neste vegg
Koden som vil gjøre nettopp dette kan se ut som følger(gitt at vi befinner oss midt på selve plata):
int i;
glTranslatef(-BOARD_WIDTH * SQUARE_SIZE / 2, 0.0, BOARD_WIDTH * SQUARE_SIZE / 2);
glPushMatrix();
for(i = 0;i < 4;i++){
glBegin(GL_QUADS);
glNormal3f(0.0, 0.0, 1.0);
glVertex3f(0.0, 0.0, 0.0);
glVertex3f(BOARD_WIDTH * SQUARE_SIZE, 0.0, 0.0);
glVertex3f(BOARD_WIDTH * SQUARE_SIZE, -SQUARE_SIZE, 0.0);
glVertex3f(0.0, -SQUARE_SIZE, 0.0);
glEnd();
glTranslatef(0.0, 0.0, -BOARD_WIDTH * SQUARE_SIZE);
glRotatef(-90.0, 0.0, 1.0, 0.0);
}
glPopMatrix();
Veggene vi tegner vil i dette tilfellet ha en høyde som er lik SQUARE_SIZE. Figur 2 og 3 viser platen med 4 vegger fra 2 forskjellige vinkler. Hvis vi nå setter et materiale på platen vår samt veggene rundt, så vil vi få noe som ligner på Figur 4. Til slutt skal denne platen ha teksturer på toppen samt på alle veggene rundt. Mer om dette senere. Jeg har med vilje valgt å ikke tegne bunnen av plata, da jeg ikke fant det nødvendig.
Kula og bevegelse
Nå som vi har en fin plate, må vi jo også ha en kule som kan trille rundt oppe på denne platen. Bare det å tegne en kule er ikke så vanskelig i seg selv, men hvis man skal få denne kula til å begynne å trille rundt etter hvor mye man tilter platen er ikke fullt så triviellt som det høres ut. For å tegne en kule så har jeg valgt å bruke en funksjon som heter gluSphere() som tegner nettopp en kule. gluSphere() tar 4 argumenter, og de er som følger:
- GLUquadric *quad
- En peker til et quadrics objekt.
- GLdouble radius
- Radiusen til kula.
- GLint slices
- Antall deler rundt z-aksen.
- GLint stacks
- Antall deler langs z-aksen.
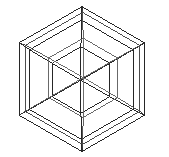
Figur 5 og 6: Kule med 6 stacks og slices

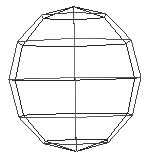
Figur 7 og 8: Kule med 50 stacks og slices
(NB! Disse kulene er tegnet med glutWireSphere() for å
vise slices og stacks mer tydelig)
quadrics objektet er et objekt man må lage med gluNewQuadric() funksjonen. Jeg valgte å sette radiusen av kula til 1/3 av SQUARE_SIZE, slik at kula blir litt mindre enn en liten firkant. De to siste argumentene vil være med på å bestemme hvor "rund" kula skal se ut. Desto høyere tall man setter, desto rundere blir kula, men desto mer kreves av maskinene for at den skal klare å tegne dette. Figur 5 og 6 viser en kule med 6 slices og stacks henholdsvis "ovenifra" og "forfra", og Figur 7 og 8 viser en kule med 50 slices og stacks henholdsvis "ovenifra" og "forfra".
Som vi ser så er det veldig stor forskjell på disse. Siden den kula som skal ligge oppe på plata kommer til å være veldig liten, så trenger man ikke mange slices og stacks for at den skal se rund ut. Siden man skal kunne zoome inn og ut i spillet, så har jeg valgt å tegne så mange som 20 slices og stacks. Dette er veldig i overkant da man som regel bare ser den lille kula med mindre man velger å zoome veldig inn. En smart løsning her kan være å ha variabel antall slices og stacks etter hvor mye brukeren har valgt å zoome slik at det tilpasser seg, men jeg ser ikke på dette som noen nødvendighet i dette tilfellet. Dette er klart noe som kan gjøres når man skal gå gjennom og optimalisere.
TokamakJeg har laget en struct som skal inneholde info om selve kula. Definisjonen på denne er som følger:
struct ball{
float x;
float y;
float z;
float rad;
float dia;
float circumf;
float rotX;
float rotZ;
float curSpeedX;
float curSpeedY;
float curSpeedZ;
};
De tre første variablene forteller hvor i koordinatsystemet kula befinner seg. Så kommer radius, diameter og omkrets. rotX og rotZ inneholder vinkelen som kula skal vri seg om x- og z- aksen for å simluere at den triller. De tre siste variablene inneholder farten som kula har i x, y og z retning. Jeg har også en struct som holder på vinklene til platen og den ser ut som følger:
struct board{
float rotX;
float rotZ;
};
rotX er hvor mye platen roterer seg om x aksen, og rotZ forteller hvor mye den skal roteres om z aksen. Brukeren kan trykke på piltastene på tastaturet for å styre platen. Mer om hvordan tastetrykk fungerer senere.
> Jeg har også valgt å sette en max verdi på hvor mye platen skal kunne tiltes slik at den ikke kan snurre helt rundt. Jeg valgte å sette denne til 5 da noe stort mer enn dette vil føre til at kula triller avgårde i rekordfart. Her følger de stegene som må til for å finne ut hvor fort kula beveger seg, og hvor mye den skal spinne:
- Trykker brukeren på noen av piltastene? Hvis så øk/minsk vinkelen som brettet tiltes i den retningen som brukeren ønsker
- Regn ut hastigheten som kula vil få på den nye vinkelen på brettet
- Legg denne nye verdien til den gamle hastigheten til kula for å få kula til å øke/minske hastigheten
- Legg hastigheten i x-retning til x posisjonen for å få en ny x posisjon til kula
- Legg hastigheten i z-retning til z posisjonen for å få en ny z posisjon til kula
- Regn ut rotasjon på kule etter hvor på platen den befinner seg
Så skal vi se på litt kode som skal utføre stegene overfor. Vi starter med å justere vinkelen til platen:
if(left_p){
if(bo.rotZ < MAX_ANGLE){
bo.rotZ += ROT_SPEED * framediff;
} else{
bo.rotZ = MAX_ANGLE;
}
}
eft_p er en int som blir satt til 1 eller 0 ettersom brukeren trykker / slipper den venstre piltasten. Hvordan dette gjøres kommer senere. Hvis det nå er tilfelle at brukeren holder venstre tasten inne, så sjekker vi først om vinkelen til brettet er mindre enn MAX_ANGLE som jeg har satt til å være 5. Hvis den er det, så legger jeg ROT_SPEED * framediff på den gamle vinkelen. Hvis den gamle vinkelen ikke er mindre enn MAX_ANGLE, så setter jeg den lik MAX_ANGLE. På denne måten vet jeg at vinkelen aldri vil overstige max verdien. ROT_SPEED er satt til å være 60, og framediff er antall sekunder mellom forrige gang denne testen ble kjørt og nå. Grunnen til at denne brukes er så platen blir tiltet omtrent like kjapt uansett hva slags maskin man sitter på. Hadde jeg valgt å bruke en konstant økning / minskning på vinkelen, ville platen ha vridd seg mye kjappere på en rask maskin siden denne testen hadde blitt kjørt oftere. For nå å øke hastigheten til vridningen av platen, så kan man øke ROT_SPEED. Koden over må da kjøres 4 ganger der man sjekker left_p, right_p, up_p og down_p og øker / minsker vinkelen til platen korrekt slik at den kan tiltes alle veier.
Når det er gjort, så kan vi regne ut hastigheten til kula på følgende måte:
b.curSpeedX += (-GRAVITY * sin(deg2rad(bo.rotZ))) / fact;
b.curSpeedZ += (-GRAVITY * sin(deg2rad(bo.rotX))) / fact;
Så skal man så godt man kan prøve å forklare de to linjene over.
GRAVITY er en konstant jeg har definert til å være 9.81. sin() er en funksjon som ligger i math.h som regner ut sinus verdien til tallet man sender som argument. Nå har det seg slik at OpenGL jobber med grader og sin() og cos() funksjonene jobber med radianer. deg2rad() er en funksjon jeg selv har definert som konverterer fra grader til radianer. Jeg har i tillegg en rad2deg() i tilfelle man skal konvertere andre veien.
For at kula skal trille mot høyre (positiv retning på x aksen) så krever det at brettet blir tiltet om z-aksen med en negativ vinkel. Det er nettopp derfor jeg bruker en negativ GRAVITY. Jeg kunne godt ha brukt -= i stedet for += og droppet minus tegnet foran GRAVITY, men jeg synes det virker mer intuitivt å gjøre det på måten beskrevet over.
Hvis brettet nå blir tiltet med en positiv vinkel om z-aksen, så vil den nye hastigheten bli negativ og b.curSpeedX vil minske. Dette gjelder også for kula når den skal bevege seg på z-aksen. For at kula skal trille utover mot brukeren (positiv retning på z-aksen), så må platen tiltes med en negativ retning om x-aksen, og motsatt hvis kula skal bevege seg i den andre retningen.
Før det nye tallet legges til b.curSpeedX og b.curSpeedZ, så blir tallet delt på fact som er en faktor jeg bruker. Grunnen til at jeg deler tallet på en faktor er for å skalere dette ned slik at bevegelsene passer til visningen på skjermen. Siden man ikke helt uten videre kan regne over fra meter pr. sekund til pixler pr. sekund så prøvde jeg meg frem med forskjellige faktorer for å få det til å se bra ut.
Nå som vi har regnet ut hastigheten til kula, så kan vi sette nye posisjoner til kula slik at den blir tegnet opp på korrekt sted. Dette kan enkelt gjøres på følgende måte:
b.x += b.curSpeedX;
b.z += b.curSpeedZ;
Her tar vi bare den nye hastigheten og plusser på posisjonen kula har fra før både i x og z retning.


Figur 9 og 10: Platen med vegger og kule
Det som nå gjenstår er å regne ut rotasjonsvinkelen som kula skal ha slik at det ser ut som den spinner rundt når den triller. Til dette bruker vi posisjonen på x og z aksen samt omkretsen til kula. De to følgende linjene regner ut dette:
b.rotZ = (b.x / b.circumf) * 360;
b.rotX = (b.z / b.circumf) * 360;
Først finner vi ut hvor mange ganger kula kan spinne en hel gang rundt ved å ta posisionen og dele på omkretsen, og så gjør vi om dette til vinkler ved å gange med 360. Dette gjøres da både på x og z verdiene til kula.
Figur 9 og 10 viser oss at platen tiltes og kula beveger seg etter vinkelen på plata.
Kassen
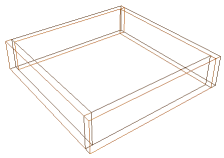
Figur 11: Kassen rundt platen
Siden det ser litt snodig ut bare med en plate som henger i løse luften så tenkte jeg jeg kunne tegne opp en kasse rundt denne platen. Kassen som blir tegnet opp består av 4 rektangulære bokser som danner en kasse. Figur 11 viser hvordan kassen ser ut. Jeg måtte passe på å ha et lite mellomrom mellom sidene på platen og innersidene på kassen slik at det ser litt mer realistisk ut. Platen blir også tegnet opp slik at toppen av platen ligger litt lavere enn toppen på kassen. Figur 12 viser kassen samt platen som ligger inni. Jeg har her satt et materiale på kassen og platen. De fire veggene på kassen blir tegnet opp på samme måte som veggene til platen bortsett fra at her bruker vi en dimensjon til, og tegner opp en rektangulær boks i stedet for bare en flate. Først tegner vi altså opp en vegg, så flytter vi origo, og roterer, så tegner vi opp neste vegg osv.
I tillegg til kassen så bestemte jeg meg for å sette på de knottene man bruker på det ekte labyrint spillet for å tilte platen. Det vil da finnes en knott i front på kassen som vil snurre om z-aksen, samt en på høyresiden som vil snurre om x-aksen. Disse knottene blir bygd opp av en sylinder samt en disk som vil fungere som et "lokk" på knotten da en sylinder hverken har topp eller bunn. Kode for å tegne knotten i front kan se slik ut(gitt at vi befinner oss midt på platen):
glPushMatrix();
glTranslatef(0.0, -bw.height / 2, ((BOARD_WIDTH / 2) * SQUARE_SIZE) + SPACE + bw.depth);
glRotatef(bo.rotZ, 0.0, 0.0, 1.0);
glMaterialfv(GL_FRONT,GL_AMBIENT_AND_DIFFUSE, knob);
gluCylinder(q, SQUARE_SIZE / 2, SQUARE_SIZE / 2, SQUARE_SIZE / 2, 20, 20);
glTranslatef(0.0, 0.0, SQUARE_SIZE / 2);
gluDisk(q, 0.0, SQUARE_SIZE / 2, 20, 1);
glPopMatrix();

Figur 12: Kasse med plate
Koden over introduserer noen nye funksjoner samt variabler som jeg selv har definert. Jeg skal forsøke å forklare disse så godt jeg kan.
bw er en struct som inneholder info om veggene til kassen. structen har tre float variabler. width, height og depth. SPACE er mellomrommet mellom platen og veggene til kassen. Det første som da skjer i koden over er at vi flytter origo fra midten av plata til midten av veggen i front. Så roterer vi slik at knotten er like "vridd" som platen er tiltet. På denne måten vil knottene bevege seg etter slik man tilter platen. Etter å ha rotert, så setter jeg et materiale slik at sylinderen og disken blir tegnet med en gitt farge. For å tegne sylinderen så bruker man en funksjon som heter gluCylinder(). Denne fungerer nogenlunde på samme måte som gluSphere(). Det første argumentet til gluCylinder() er et quadrics objekt. Argument 2 og 3 er radius til henholdsvis bunn og topp av sylinderen. De to siste argumentene til funksjonen er hvor mange slices og stacks man skal bruke for å tegne den opp. Hvis man går tilbake til å se på hvordan vi tegnet opp kula så står disse forklart der. Referer til Figur 5-8 for å se hvordan disse henger sammen med hvordan objektet blir tegnet opp.
Etter vi har tegnet opp sylinderen, så flytter vi origo ut til toppen av sylinderen vi nettopp tegnet for å legge på plass en disk her, slik at knotten blir lukket. Funksjonen som tegner en disk ligner også på gluSphere(). Det første argumentet er et quadrics objekt, det andre er den innerste radiusen til disken, og det tredje er den ytterste radiusen. Siden vi vil ha en lukket disk setter vi 0.0 på den innerste radiusen. De to siste argumentene er slices og loops. Slices forteller hvor manger deler rundt z-aksen vi skal tegne, og loops forteller hvor mange konsentriske ringer rundt utgangspunktet som disken er delt opp i. Og til slutt popper vi matrise stacken for å komme oss tilbake til slik det var før vi startet å tegne knotten.

Figur 13: Kasse med plate og knotter
For å tegne den andre knotten så gjøres det på akkurat samme måte bortsett fra at vi har et ekstra kall til glRotatef() der vi roterer oss negative 90 grader om y aksen for å kunne tegne på høyreveggen til kassen.
Figur 13 viser kassen med plate og knotter og det hele.
Nå som vi har en finfin kasse med en plate som kan tiltes og en kule og det hele, så må vi legge noen labyrinter på denne platen slik at kula har noen vegger å treffe.
Labyrinter og kollisjoner
222222
211112
211112
211112
211112
222222
så kan vi si at der tallet er 2, så skal vi tegne en flate med en vegg oppå, og der det står 1 skal vi kun tegne en flate. Vi hadde derfor fått en plate med en solid vegg rundt hele. For å kunne tegne opp noe slikt så kan vi trikse litt med koden som tegner opp 20x20 firkanter som står nevnt tidligere. Siden vi nå skal tegne i 2 lag på y-aksen så må vi ha en løkke rundt det hele som går nettopp 2 ganger. Og for hver firkant vi skal tegne, så må vi gjøre et oppslag i int arrayet vårt for å se hva vi faktisk skal tegne. Under kommer kode som kan gjøre dette for eksempelkartet over:
for(y = 0;y < 2;y++){
if(i == 0){
/* første nivå, kun flater skal tegnes */
for(z = 0;z < 6;z++){
for(x = 0;x < 6;x++){
drawFloor(x, z);
}
}
} else{
/* andre nivå, må se etter vegger */
for(z = 0;z < 6;z++){
for(x = 0;x < 6;x++){
if(map[z][x] == 2){
drawWall(x, z);
}
}
}
}
}
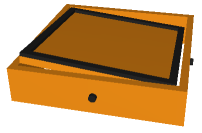
Figur 14: Kasse med plate,
knotter og en "labyrint"
Koden over er ikke fullstendig, men forklarer hvordan dette kan løses på en grei måte. Man tegner først opp et brett, og så går man gjennom map arrayet, og tegner vegger der de skal være. drawFloor() og drawWall() kan da være funksjoner som tegner opp flater og vegger på korrekt sted. Figur 14 viser hvordan det hele ser ut med en "labyrint" på plata.
Og nå kommer den litt hårete delen. Nå skal vi få kula til å "kollidere" med veggene slik at den ikke bare triller rett gjennom de. Vi kommer til å måtte regne litt for å få til dette, men ingen grunn til å slutte å lese her av den grunn. Matte er jo bare artig! :)
Koden som nå følger vil sjekke om kula treffer en vegg når den triller mot venstre (i negativ retning på x aksen):
if(b.curSpeedX < 0){ /* going left */
x = (int)(((b.x - b.rad) / SQUARE_SIZE) + (BOARD_WIDTH / 2));
z = (int)((b.z / SQUARE_SIZE) + (BOARD_WIDTH / 2));
if(map[z][x] == 2){
b.curSpeedX = 0;
b.x = (x * SQUARE_SIZE) - (SQUARE_SIZE * BOARD_WIDTH / 2) + SQUARE_SIZE + b.rad;
}
}
Og så skal vi prøve å forklare litt igjen. Det første som skjer er en if test som sjekker om hastigheten til kula på x-aksen er mindre enn null. Hvis den er det, så beveger altså kula seg mot venstre. Vi går utifra at SQUARE_SIZE og BOARD_WIDTH er henholdsvis 0.075 samt 20 (som nevnt tidligere). Det vi nå må gjøre er å regne ut hvilken "firkant" på brettet som venstre "kant" kula befinner seg på. Altså midtpunktet på kula minus radiusen. Når vi da vet hvor på brettet dette punktet er kan vi gjøre et oppslag i int arrayet som inneholder kartet og sjekke om punktet ligger på en firkant som inneholder en vegg. Hvis dette er tilfellet, må hastigheten til kula på x-aksen bli satt til 0, og for sikkerhets skyld så flytter vi kula slik at den ligger helt inntil veggen.
For å finne ut hvilken firkant på x-aksen dette punktet befinner seg, så gjøres følgende:
- Kula sin x posisjon minus kula sin radius (posisjonen til venstre "kant")
- Del dette tallet på SQUARE_SIZE for å finne hvor mange firkanter denne posisjonen utgjør
- Legg til BOARD_WIDTH / 2 siden int arrayet går fra 0 og oppover, mens 0 i koordinatsystemet er i midten
- Cast denne verdien til en int for å finne posisjon i int arrayet
Dette gjøres også for z posisjonen, men her trenger vi ikke vite noe om venstre "kant" men bare hvor på z-aksen midtpunktet befinner seg. Koden som regner ut den nye posisjonen til kula på x-aksen er nesten motsatt av koden som finner ut hvilken posisjon i int arrayet kula befinner seg på. Brukeren vil aldri se at kula blir lagt tilbake slik at den ligger helt inntil veggen. Grunnen til at dette gjøres er at når kula beveger seg veldig fort på platen, så kan "stegene" som den beveger på bli såpass store at kula havner midt inne i en vegg.
Koden over sjekker kun når kula beveger seg mot venstre, så man må også teste i de andre retningene. Jeg kommer ikke til å skrive koden for det her, da det gjøres på akkurat samme måte som det jeg nettopp har beskrevet, bare at man bytter om hvilke punkter man skal sjekke på. Når alle disse er på plass, så har man da litt generell kollisjonsbehandling på plass. Det er nå likegyldig hvor på brettet labyrinten ligger. Koden vil uansett finne ut om kula krasjer i en vegg. Nå som vi har selve labyrinten på plass, så kan vi begynne med å tegne noen hull. Det må nevnes med en gang at hull ikke er helt implementert i min versjon av Labyrinten. Kode som tegner opp hull på platen er på plass, men kula bryr seg ikke om den. Triller den over et hull, så er det ikke noe spesielt som skjer. Men siden bare det å få fine hull på platen ikke var så lett så tar jeg det med uansett.
Hull
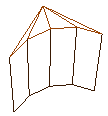
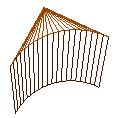
Figur 15 og 16: Hjørne i et hull
med nøyaktighetsgrad 4 og 20
Det første vi kan gjøre er å utvide kartet vårt litt slik at vi kan sette inn et tall som skal gjengi hull i platen. Til dette har jeg valgt 0 da tallet både ligner og rimer på hull. :) Hvis vi ser for oss et kart på 6x6 som ser slik ut:
222222
211112
210112
211012
211112
222222

Figur 17: Labyrint med hull
så ser vi at vi her ville ha fått et brett med en vegg rundt, samt to hull. For å få tegnet opp dette så må vi utvide koden over som tegner opp flater og vegger. Det vi må gjøre er å legge til en if test som sjekker om vi skal tegne flater eller hull på første nivå av brettet. Jeg har laget en funksjon som tegner opp slike hull. Måten jeg gjør det på er at jeg har en løkke som går 4 ganger som tegner opp hvert hjørne i hullet for seg med en gitt nøyaktighets grad. Nøyaktighetsgraden kan da være variabel etter hvor mye man har zoomet inn/ut, men jeg har valgt å fastsette denne til 10 da dette ser bra nok ut selv om man zoomer langt inn. Hvis vi tar en titt på figur 15 og 16, så vil vi se et hjørne av hullet først med nøyaktighetsgrad 4 og så 20. Nøyaktighetsgraden forteller da hvor mange triangler jeg har brukt for å tegne opp et hjørne i hullet. Vi ser også at det blir tegnet opp firkanter nedover slik at man får noe som ligner en sylinder. Hvis vi nå skal ta for oss en funksjon som kun skal tegne opp toppen av hullet, altså bare trekantene, så kan den se ut som Fig 17.
void drawHole()
{
coord2D x1,x2,x3;
int i, step, numsteps = 4;
float center = SQUARE_SIZE / 2;
x1.x = x1.z = 0.0;
for(i = 0;i < 4;i++){
x2.x = 0.0;
x2.z = center;
for(step = 1;step <= numsteps;step++){
x3.x = center + cos(M_PI + (M_PI / (2 * numsteps))*step) * center;
x3.z = center + sin(M_PI + (M_PI / (2 * numsteps))*step) * center;
glBegin(GL_TRIANGLES);
glNormal3f(0.0, 1.0, 0.0);
glVertex3f(x1.x, 0.0, x1.z);
glVertex3f(x3.x, 0.0, x3.z);
glVertex3f(x2.x, 0.0, x2.z);
glEnd();
x2.x = x3.x;
x2.z = x3.z;
}
glTranslatef(SQUARE_SIZE, 0.0, 0.0);
glRotatef(-90, 0.0, 1.0, 0.0);
}
}
Vi tar her utgangspunkt i at origo er satt til å være i øvre venstre hjørnet av hullet. Først har vi en løkke som går fra 0 til 4. Det er denne løkka som gjør at vi kan tegne 4 hjørner. Siden trianglene vi skal tegne ligger på samme flate, trenger vi ikke ta hensyn til y-aksen i utregningene. Inne i løkka som går fra 0 til 4 har vi en løkke som går fra 1 til numsteps. numsteps er da en variabel som forteller hvor nøyaktig dette skal tegnes opp. Inne i den løkka igjen, så regner vi ut de punktene som vi skal tegne triangler om. Når den innerste løkka er ferdig, så flytter vi origo og roterer, slik at vi kan tegne neste hjørne. En ulempe med denne metoden er at hvis man skal ha en tekstur på hele platen, så er det vanskelig å få til å tegne teksturen på de triangele som bygger opp et hull. Jeg har utelatt dette da jeg uanset ikke ble ferdig med implementeringen av hull. Figur 17 viser en labyrint med noen hull.
Nå går vi over til hvordan vi kan få på plass noen teksturer slik at det hele kan se mye bedre ut.
Teksturer
Jeg kommer ikke til å gå så veldig i dybden på dette temaet her, så litt kjennskap til hvordan teksturer fungerer i OpenGL anbefales.
De teksturene jeg har brukt til spillet har jeg funnet på http://astronomy.swin.edu.au/~pbourke/texture/. Der finnes det mange forskjellige teksturer man kan prøve seg frem med. Jeg fant et par fine som så litt ut som treverk. Siden det hadde vært litt tamt å bruke den samme teksturen på alle veggene, så klippet jeg ut noen forskjellige fra det ene bildet jeg fant. På den måten så ser det ikke ut som alt er prikk likt i alle fall.
Først og fremst har jeg en funksjon som heter loadTextures() som blir kjørt i init() funksjonen som laster inn alle teksturer brukt i spillet. Denne funksjonen bruker en annen funksjon som heter imageLoad() som laster inn selve bildet. loadTextures() genererer ider til teksturene slik at jeg lett kan referere til dem senere i koden. Jeg har valgt å legge 4 forskjellige teksturer på veggene på kassen, samt en egen tekstur oppe på platen. Teksturene som legges på veggene gjøres på helt vanlig måte. Man gjør et kall til glBindTexture(), som da binder en gitt tekstur til det man skal tegne, og så setter man tekstur koordinater på vanlig måte på de fire veggene til kassen. Når man skal til å legge en tekstur på platen, så blir det litt mer jobb. Platen er ikke bare en stor firkant, men den er bygd opp av 20x20 mindre firkanter. Derfor må små deler av teksturen settes på hver av disse små firkantene. Funksjonen jeg har som tegner opp flatene ser slik ut:
void drawFloor(int x, int z)
{
glBindTexture(GL_TEXTURE_2D,texture[4]);
glBegin(GL_QUADS);
glNormal3f(0.0, 1.0, 0.0);
glTexCoord2d(0.0 + (x / (float)BOARD_WIDTH), 1.0 - (z / (float)BOARD_WIDTH)); glVertex3f(0.0, 0.0, 0.0);
glTexCoord2d(0.0 + ((x + 1) / (float)BOARD_WIDTH), 1.0 - (z / (float)BOARD_WIDTH)); glVertex3f(SQUARE_SIZE, 0.0, 0.0);
glTexCoord2d(0.0 + ((x + 1) / (float)BOARD_WIDTH), 1.0 - ((z + 1) / (float)BOARD_WIDTH)); glVertex3f(SQUARE_SIZE, 0.0, SQUARE_SIZE);
glTexCoord2d(0.0 + (x / (float)BOARD_WIDTH), 1.0 - ((z + 1) / (float)BOARD_WIDTH)); glVertex3f(0.0, 0.0, SQUARE_SIZE);
glEnd();
}

Figur 18: Teksturer
Denne funksjonen tar 2 argumenter, og det er x og z posisjonen som denne firkanten skal tegnes på. Disse blir sendt med fra løkken som går gjennom kartet og tegner opp flater, vegger, hull osv.
Det første som skjer i drawFloor() er et kall til glBindTexture(). texture er et egendefinert int array som man kan bruke for å referere til de forskjellige teksturene. I dette tilfellet vil jeg bruke den teksturen som texture[4] referer til, og det er nettopp den teksturen som skal ligge på platen. Når jeg nå skal bestemme punktene i firkantene, så må jeg først sette en teksturkoordinat, som da vil bli mappet til det punktet som følger. Siden jeg vet hvor på platen denne firkanten skal tegnes, så kan jeg også regne meg frem til hvor på teksturen dette tilsvarer. Når det gjelder hullene så har jeg som sagt ikke implementert mapping av teksturer på trianglene i hjørnene, men dette er ikke synlig med mindre man zoomer veldig mye inn. Figur 18 viser kassen og platen med teksturer. Ser det ikke pent ut? :)
Generering av brett
For å generere forskjellige brett så har jeg valgt å først tegne de opp ved hjelp av tallene 0,1,2 og 3 der 0 betyr hull, 1 betyr flate, 2 betyr vegg og 3 er der kula skal plasseres. Alt som da ligger i brett filene, skal legges inn i int arrayet vårt som jeg har nevnt tidligere. Dette gjøres da ved å lese en og en byte fra filen, gjøre om byten til et tall, og sette det inn i arrayet. Kartet man skal bruke sendes da med som argument til programmet, og det første som programmet gjør er å populere int arrayet utifra hvilken fil man spesifiserer. Grunnen til at jeg valgte denne løsningen er fordi det er lett å tegne opp kart og teste ut forskjellige labyrinter osv, og den kan lett utvides slik at man kan sette på plass andre objekter ved å sette inn andre tall eller tegn i filen.
Tastetrykk og musebevegelser
Platen til spillet kan styres via piltastene på tastaturet, og scenen kan roteres ved å trykke ned en knapp på musen, og så bevege den. For å kunne behandle taste- og musetrykk med Glut, så må man sette opp forskjellige keyhandlere og mousehandlere. De funksjonene man setter opp vil da motta som argument hva brukeren trykker på evt. koordinatene til musen hvis den beveger seg. Dette kan gjøres i main() funksjonen, og jeg har valgt å gjøre det på følgende måte:
glutKeyboardFunc(keyhandler);
glutKeyboardUpFunc(keyuphandler);
glutSpecialFunc(skeyhandler);
glutSpecialUpFunc(skeyuphandler);
glutMouseFunc(mouseClick);
glutMotionFunc(mouseMovement);
Her setter jeg opp at en funksjon som heter keyhandler() skal ta seg av vanlige tastetrykk på tastaturet, og keyuphandler() skal ta seg av det som skjer når noen slipper en tast på tastaturet. De fleste av disse fungerer veldig likt, så jeg kommer ikke til å ta for meg alle sammen her. Jeg kan vise hvordan keyhandler() kan få til å avslutte programmet ved å trykke på q tasten på tastaturet. Her følger et eksempel på hvordan keyhandler() kan se ut:
void keyhandler(unsigned char key, int x, int y)
{
switch(key){
case 'q': exit(0); break;
}
}
Her ser vi at vi får inn 3 argumenter. Den første er hvilken tast brukeren har trykket på, og de to andre forteller hvor på skjermen pekeren til brukeren befinner seg. Det eneste vi er ute etter i dette tilfellet er hvilken tast brukeren har trykket på. Dette kan sjekkes ved hjelp av en switch case struktur. Når man skal legge til støtte for flere tastetrykk er det bare å legge til flere case.
keyhandler() tar ikke for seg alle tastene på tastaturet. "Spesielle" taster som f.eks piltastene må behandles av den funksjonen man sender med i glutSpecialFunc(). Den funksjonen man velger å bruke til dette vil være nesten identisk med keyhandler() funksjonen. Som avslutning så lister jeg opp hvilke taster jeg har satt opp i spillet:
| q | Avslutt |
| z | Zoom inn |
| x | Zoom ut |
| 0 | Nullstill platen |
| v | Slå av/på utskrift av FPS(frames pr. sekund) |
| Venstre piltast | Tilte brettet til venstre |
| Høyre piltast | Tilte brettet til høyre |
| Øvre piltast | Tilte brettet opp |
| Nedre piltast | Tilte brettet ned |
Og det var det. Spillet er skrevet i C og jeg har brukt Glut. Det er noe kommentarer i koden(på engelsk), men for de som ikke har sett på C før, så kan det bli tungt. Det har blitt utviklet på en Pentium Centrino 1500 med et ATI Radeon 9000 M skjermkort. Jeg oppnår ~200FPS under kjøring på min maskin, men bare ~10 på en maskin her på skolen.
Jeg må si at dette er uten tvil det artigste faget jeg noensinne har hatt, og jeg kommer til å fortsette å holde på med OpenGL i tiden fremover. Jeg håper denne teksten har vært nyttig og at de som har lest den har fått noe ut av det. :)

