Vannflate
Eg vil presentere tre framgangsmåtar for å modellere vatn: samansatte "vanlige" flater, Bézierflater og NURBS og vise programmeringsteknikkar som kan brukast for å få slike flater til å likne på vatn. På grunn av tidsbegrensningar så har eg valgt å fokusere på å få naturlige bevegelsar i vatnet, ikkje på å få flatene mest mulige like materialet vatn vha. textures, blending og/eller lyssetting.
Demoapplikasjonen er skriven i C og brukar GLUT som OpenGL-bibliotek.
Flater
Vannflater har, som dei fleste andre reelle objekt, bortimot uendelig kompleksitet. Dette medfører at vi på ei datamaskin berre kan gjenskape ei tilnærming av objektet. For å få denne tilnærminga best mulig gjeld det å finne dei mest distinkte særtrekka ved objektet vi skal gjenskape. La oss fyrst lage ei liste over kva som visuelt kjenneteiknar ei vannflate i bevegelse.

Vi ser at:
- Vannflata er i konstant bevegelse i høgderetninga med varierande tempo og amplitude.
- Bevegelsane er tilsynelatande tilfeldige, det er iallefall sjeldan eit mønster gjentek seg.
- Vannflata er svært lysreflektiv.
Det siste punktet ser vi bortifrå, men dei to fyrste er viktige og vi vil jobbe med desse som mål.
Med dette som utgangspunkt kan vi gjere vårt fyrste spede forsøk på å modellere ei vannflate i OpenGL.
void display(void)
{
GLfloat mat[16][16][3];
GLint i, j;
static GLdouble incr = 0;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glMatrixMode(GL_MODELVIEW);
glEnable(GL_SMOOTH);
glClearColor(1, 1, 1, 1);
glColor3f(0, 0, 1);
gluLookAt(20, 4, 12, 0, 0, 0, 0, 1, 0);
/* Fyll matrisa */
for(i=0; i < 16; i++) {
for(j=0; j < 16; j++) {
incr += 0.005;
mat[i][j][0] = j - (16/2);
mat[i][j][1] = sin(incr*10);
mat[i][j][2] = i - (16/2);
}
}
/* Teikn opp flater mellom punkta */
for(i=0; i < 15; i++) {
glBegin(GL_QUADS);
for(j=0; j < 15; j++) {
glVertex3f(mat[i][j][0], mat[i][j][1], mat[i][j][2]);
glVertex3f(mat[i+1][j][0], mat[i+1][j][1], mat[i+1][j][2]);
glVertex3f(mat[i+1][j+1][0], mat[i+1][j+1][1], mat[i+1][j+1][2]);
glVertex3f(mat[i][j+1][0], mat[i][j+1][1], mat[i][j+1][2]);
}
glEnd();
}
glutSwapBuffers();
}
Komplett kode her
Vi brukar her matrisa mat som kontrollpunktmatrise. Den har 16 * 16 punkt i tre dimensjonar og vi fyller kvar rad i denne med lineært stigande verdiar i x-retning, eit produktet av ein sinus-funksjon i y-retning og 1 i auke for kvart steg i z-retning. Dette gir oss ei kvadratisk flate i x- og z-retning, med "rullande" høgde i y-retning. Vi teiknar så opp rektangel etter følgande oppskrift:
For kvar kolonne (a) i kvar rad (b) teikn eit rektangel med hjørner i punkta (a,b), (a, b+1), (a+1, b+1) og (a+1, b).
Og får ei skvulpande flate som ser omtrent slik ut.

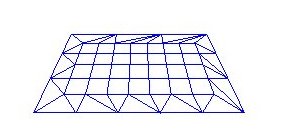
Det som blir gjort i dette programmet er å teikne opp eit stort antal småflater som til saman gir inntrykk av å vere ei større ujamn flate. Bølgebevegelsen kjem frå dei varierande y-verdiane i matrisa som blir rekna ut vha. ein sinus-funksjon for kvar rendring. Om vi teiknar ut flata som enkle linjer ser vi enklare strukturen på flata:
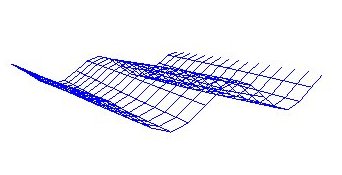
Men det som fort viser seg er at å rekne ut eit stort nok antal punkt til å gjere ei slik plate glatt blir tungvint. Vi treng ein enklare måte å modellere flate, helst ei metode som muliggjer ei relativt lita matrise av kontrollpunkt og som teiknar glatte fine kurver mellom desse punkta. Ein måte å oppnå desse krava er ved å bruke Bézierflater.
Bézierflater
Bézierflater og Bézierkurver har sitt navn frå den franske ingeniøren Pierre Bézier som presenterte konseptet i 1962. Bézier brukte denne typen kurver til å designe bilkarosseri og hadde tatt utgangspunkt i de Casteljau's algoritme (presentert av Paul de Casteljau i 1959). Bézierkurver er i dag ein av dei mest anvendte metodene innan grafisk databehandling for å visualisere kurver og flater.
Ei Bézierkurve tek si form etter eit sett kontrollpunkt som angir kvar kurva skal gå i det todimensjonale planet eller tredimensjonale rommet. Det er viktig å merke seg at kurva nødvendigvis ikkje går gjennom alle desse kontrollpunkta, men at alle kontrollpunkta har innvirkning på den endelige kurva. La oss ta eit eksempel basert på ei kurve med fire kontrollpunkt: A, B, C og D.
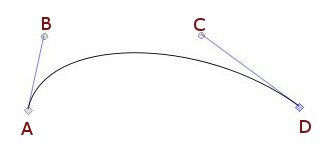
Vi ser at den deriverte i punktet A har lik stigningsgrad som linja A-B, den deriverte av kurva i punktet midt mellom B og C har lik stigningsgrad som linja B-C og at den deriverte i D har lik stigningsgrad som linja C-D. I praksis er dette den effekten kontrollpunka har på ei Bézierkurve og vi nøyer oss med å konstatere at slik er det, utan å gå vidare inn på teorien bak (sjå WikiPedia for meir informasjon). Men kun kurver er ikkje nok til å modellere vatn, vi treng Bézierflater og korleis fungerer dei? Jo, Bézierflater i OpenGL kan ein enkelt forestille seg ved å sjå for seg fleire Bézierkurver ved sidan av kvarandre i rommet med kvadratiske eller triangulære flater dratt mellom punkta på kurvene i ei valgt oppløysing. La oss prøve å programmere ei slik flate.
void display(void)
{
#define ARRSIZE 8
GLfloat mat[ARRSIZE][ARRSIZE][3];
GLint i, j;
static GLdouble incr = 0;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glMatrixMode(GL_MODELVIEW);
glEnable(GL_SMOOTH);
glClearColor(1, 1, 1, 1);
glColor3f(0, 0, 1);
gluLookAt(8, 4, 8, 0, 0, 0, 0, 1, 0);
/* Fyll matrisa */
for(i=0; i < ARRSIZE; i++) {
for(j=0; j < ARRSIZE; j++) {
incr += 0.005;
mat[i][j][0] = j - (ARRSIZE/2);
mat[i][j][1] = sin(incr*100);
mat[i][j][2] = i - (ARRSIZE/2);
}
}
/* Slå på nødvendige OpenGL-features */
glEnable(GL_MAP2_VERTEX_3);
glEnable(GL_AUTO_NORMAL);
/* Evaluer kontrollpunktmatrisa */
glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, ARRSIZE,
0, 1, ARRSIZE*3, ARRSIZE, &mat[0][0][0]);
/* Teikn ei 20 * 20 punkts flate */
glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
glEvalMesh2(GL_LINE, 0, 20, 0, 20);
glutSwapBuffers();
}
Komplett kode her
Dette programmet liknar det fyrste eksempelet, bortsett frå at vi her evaluerer ei 8 * 8 kontrollpunktmatrise før vi teiknar ei 20 * 20 punkts Bézierflate på bakgrunn av denne kontrolpunktmatrisa. Men vi har også lagt til ein heil del nye funksjonar, la oss gå gjennom dei ein for ein.
-
glEnable(GL_MAP2_VERTEX_3);
Etter dette vil kall til glEvalMesh() teikne punkt i tre dimensjonar.
-
glEnable(GL_AUTO_NORMAL);
Denne sikrar at det vil bli lagt normalar på Bézierflata, så lenge vi ikkje jobbar med materialer og lys så er ikkje dette så viktig, men det er ein god ide å ha denne satt til seinare. Normalar er det som angir kva som er framside/utside/innside på eit objekt.
-
glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, ARRSIZE, 0, 1, ARRSIZE*3, ARRSIZE, &mat[0][0][0]);
Dette er funksjonen som faktisk evaluerer punkta vi har i kontrollpunktmatrisa, argumenta angir i hovudsak størrelsen på matrisa i kvar retning, adressa til matrisa og avstanden mellom kvart vertex i matrisa.
-
glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);
Angir at punkta frå glMap2f() skal bli evaluert over ei 20 * 20 punkts matrise med lineært forhold mellom punkta i kvar retning.
-
glEvalMesh2(GL_LINE, 0, 20, 0, 20);
glEvalMesh() teiknar punkta/linjene/flatene i Bezièrflata i den angitte størrelsen.
Vi teiknar flata med GL_LINE istadenfor GL_FILL som argument til glEvalMesh2() og får difor berre linjene mellom punkta i flata istadenfor ei fylt flate. Resultatet ser slik ut.
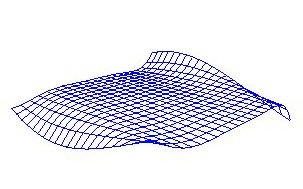
No begynner flata vår å likne vatn. Kurvene er glatte og bevegelsane relativt naturlige, men for å få ei større vannflate som framleis er truverdig så treng vi ei større kontrollpunktsmatrise, og her støter vi på eit problem. Bezièrflater er nemlig såpass tunge å kalkulere at dersom vi prøver med kontrollpunktsmatriser på 16 * 16 * 3 eller 24 * 24 * 3 punkt så vil applikasjonen vår fort knele gjennomsnittlige datamaskiner. Antallet kontrollpunkt vil bli så stort at datamaskina ikkje rekk å teikne flata mange nok gongar i sekundet og vi vil oppleve enten hakking i biletet eller at flata tilsynelatande er seig som sirup.
NURBS
Basics
NURBS står for Non-Uniform Rational B-Splines og skiller seg frå Bezièrkurver/Bezièrflater ved at dei er betraktelig raskare å rekne ut og at dei i tillegg til ei kontrollpunktmatrise også brukar ei "knutematrise" som angir kor stor påvirkning eit kontrollpunkt skal ha på eit gitt punkt på kurva. Fokus for dette avsnittet blir praktisk bruk av NURBS og hensiktsmessig manipulering av kontrollpunktsmatriser. Teorien bak NURBS er relativt tung og eg går ikkje inn på den her. Eg forutset at lesaren har ei viss forståing av NURBS før han les denne delen av rapporten. Å ha lest og forstått Børre Stenseths NURB'er er ein bra basis.
Vi går rett på og lagar ei flat NURBS-flate, for å sjå kva som må til:
void display(void)
{
#define NUMKNOTS 8
static GLfloat ctpnts[8][8][3];
static GLfloat knots[NUMKNOTS];
GLint i, j;
GLUnurbs *nobj;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glMatrixMode(GL_MODELVIEW);
glEnable(GL_SMOOTH);
glClearColor(1, 1, 1, 1);
glColor3f(0, 0, 1);
gluLookAt(0, 2, 6, 0, 0, 0, 0, 1, 0);
glTranslatef(-1.5, 0, 0);
for(i=0; i < 8; i++) {
for(j=0; j < 8; j++) {
ctpnts[i][j][0] = j;
ctpnts[i][j][1] = 0;
ctpnts[i][j][2] = i;
}
knots[i] = i;
}
nobj = gluNewNurbsRenderer();
gluNurbsProperty(nobj, GLU_DISPLAY_MODE, GLU_OUTLINE_POLYGON);
gluBeginSurface(nobj);
gluNurbsSurface(nobj, NUMKNOTS, knots, NUMKNOTS, knots, 8*3, 3, ctpnts, 4, 4, GL_MAP2_VERTEX_3);
gluEndSurface(nobj);
gluDeleteNurbsRenderer(nobj);
glutSwapBuffers();
}
Komplett kode her
Overraskande nok ser vi at det faktisk ikkje er særlig mykje meir kode som skal til for å få laga ei NURBS-flate. Det som skiller seg ut er at vi må lage ein knots-array som skal halde knute-rekkefølga, men sidan vi skal ha ei smooth og jamn overflate så er vi best tjent med at denne knute-arrayen er lineær og vi fyller den difor med stigande verdiar frå 0 til 7.
Følgande steg er nødvendig for å lage ei NURBS-flate:
-
gluNewNurbsRenderer();
gluNewNurbsRenderer() gir GLUnurbs-objektet ein unik ID som vi seinare kan bruke for å sette properties på flata.
-
gluNurbsProperty(nobj, GLU_DISPLAY_MODE, GLU_OUTLINE_POLYGON);
Denne er relativt sjølvforklarande, den set nobj sin display-mode til å vere GLU_OUTLINE_POLYGON som innebærer at kun linjene mellom punkta i NURBS-flata blir vist.
-
gluNurbsSurface(nobj, NUMKNOTS, knots, NUMKNOTS, knots, 8*3, 3, ctpnts, 4, 4, GL_MAP2_VERTEX_3);
gluNurbsSurface() er den funksjonen som faktisk teiknar NURBS-flata. Argumenta gir størrelsane og adressene til både knute-arrayen og kontrollpunktmatrisa, i tillegg til informasjon om avstanden mellom vertexpunkta i listene
Kompilerer og kjører vi programmet får vi følgande:
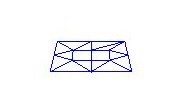
Som vi ser er flata overraskande enkel med tanke på mengda kontrollpunkt, men flyttar vi oss nærmare flata (ved å forandre linja gluLookAt(0, 2, 6, 0, 0, 0, 0, 1, 0); til gluLookAt(0, 1, 3.5, 0, 0, 0, 0, 1, 0);) ser vi noko interessant:
Flata har tilsynlatande fått fleire kontrollpunkt. Dette er OpenGL-biblioteket som sjølv justerer granulariteten i flata avhengig av avstanden til kamera. Det forklarer kvifor NURBS i mange tilfeller er betraktelig raskare enn Bezièrflater.
Modulator-funksjonen
No har vi flata og neste steg er å få bevegelse i den. Som i eksempla tidligare endrar vi kun på y-koordinaten i kontrollpunktmatrisa, men denne gongen lagar vi ein eigen modulator-funksjon som endrar alle y-koordinatane i matrisa før kvar rendring. Modulator-funksjonen skal ta imot eit amplitude argument som bestemmer maksimal variasjon på y. For å få ein naturlig bevegelse i bølgene er det lurt å bruke produktet av amplituden og sinus av ein løpeverdi. Her er eit eksempel på ein heilt enkel slik modulator-funksjon:
void modulator(GLfloat *ctpnts, GLint arrsize, GLdouble ampl)
{
GLint i, j;
static GLdouble incr = 0;
for(i=0; i < arrsize; i++) {
for(j=0; j < arrsize; j++) {
incr += 0.0001;
ctpnts[(i*arrsize*3) + (j*3) + 1] = ampl*sin(i+j+incr);
}
}
}
Komplett kode her
Etter å ha sendt kontrollpunktmatrisa gjennom denne funksjonen nokre gongar ser Bezièrflata slik ut:
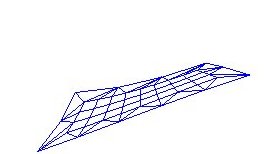
For å få meir komplekse bølgebevegelsar kan ein kombinere fleire sinus-funksjonar, f.eks
ctpnts[(i*arrsize*3) + (j*3) + 1] = ampl*sin(i+j+incr) + ampl*sin(i*j*incr);
Modulator-funksjonen er ein av dei mest avgjerande faktorane når ein skal prøve å modellere ei vannflate, og å bruke tid for å få den bra kan vere gull verdt.
Demoapplikasjonen

I demoapplikasjonen min, kreativt kalt Water, har eg prøvt å benytte meg av alt eg har lært om NURBS og modellering av vannflater og laga ein applikasjon der brukaren kan forandre på dei fleste parametra for å sjå effekten i praksis. Applikasjonen består enkelt og greit av ei NURBS-flate og ei lita øy, for å vise korleis ei slik vannflate kan brukast i praksis. Alle aspekt ved NURBS-flata omtalt i denne rapporten kan editerast frå brukaren sitt tastatur.
Følgande tastaturbindingar er satt opp:
| Tast | Funksjon |
| w | Flytt kamera i negativ z-retning ("innover" i landskapet). |
| s | Flytt kamera i positiv z-retning ("utover" i landskapet). |
| d | Flytt kamera i positiv x-retning (til venstre). |
| a | Flytt kamera i negativ x-retning (til høgre). |
| q | Flytt kamera i positiv y-retning (oppover). |
| e | Flytt kamera i negativ y-retning (nedover). |
| Space | Slå av/på rotering rundt senter, |
| k | Slå av/på fylling av vannflata. |
| l | Slå av/på teikning av øya. |
| p | Slå av/på teikning av kontrollpunkt i bølgene. |
| c | Slå av/på teikning av linjer mellom kontrollpunkta i bølgene. |
| + | Auk bølgeamplituden. |
| - | Senk bølgeamplituden. |
| * | Auk bølgehastigheita. |
| / | Senk bølgehastigheita. |
| m | Auk antalet kontrollpunkt i bølgene. |
| n | Senk antalet kontrollpunkt i bølgene. |
| 1 | Bruk bølgefunksjon 1. |
| 2 | Bruk bølgefunksjon 2. |
| 3 | Bruk bølgefunksjon 3. |
| 4 | Bruk bølgefunksjon 4. |
| 5 | Bruk bølgefunksjon 5. |
| r | Sett alle instillingar tilbake til utgangspunktet. |
| v | Skriv ut tilleggsinformasjon om framerate, antal kontrollpunkt osv. |
| Escape | Avslutt. |
Bølgene
Bølgene består av ei enkel NURBS-flate som blir modifisert av modwater() for kvar frame. Justeringa er tidsuavhengig så tempoet på bølgene skal vere det samme uansett CPU/grafikkort, men frameraten blir nødvendigvis dårligare på treigare utstyr. Bølgene sin utsjånad og oppførsel er bestemt av ein struct state:
typedef struct {
GLint numCtrlPts; /* Antal kontrollpunkt i kvar retning av kontrollpunktmatrisa */
GLfloat waveAmplitude; /* Bølgehøgde */
GLfloat waveSpeed; /* Bølgefart */
GLint modFunc; /* Bølgefunksjon */
bool useWire; /* Teikn kun bølgelinjene */
bool circulate; /* Sirkuler rundt senter */
bool showCtrlLines; /* Teikn linjer mellom kvar kontrollpunkt */
bool showCtrlPts; /* Vis kontrollpunkt */
bool showEnviron; /* Vis øya */
bool verbose; /* Skriv ut tilleggsinformasjon */
} state;
Med relativt høg waveAmplitude og useWire, showCtrlPts og showCtrlLines satt til true kan bølgene sjå f.eks sånn ut:

Øya
For å vise korleis vannflater kan sjå ut i praksis har eg laga ei lita øy i havet. Øya er ikkje synlig i utgangspunktet, men kan gjerast synlig ved å trykke 'l'. Prøv for eksempel å trykke 'l', for å vise øya, og 'k', for å rendre havet fylt og med farge.
Øya er ei Bezièrflate med eit grastexture på. Formen blir ikkje rekna ut, men er statisk modellert.
For seg sjølv så ser øya slik ut.

Timing
Eit vanlig problem når ein utviklar modellar som er i bevegelse, er at bevegelsane vil gå fortare jo raskare maskin applikasjonen kjører på. For å bøte på dette problemet må vi ta tida til hjelp. I staden for å flytte oss ein konstant avstand og teikne opp så ofte maskinvaren tillet, så teiknar vi opp så ofte maskinvaren tillet, men flyttar oss ein konstant avstand ganga med ein tidsfaktor. Følgande pseudokode illustrerer konseptet:
currentTime = getCurrentMilliSec(); move(distance * (currentTime - previousTime)); previousTime = currentTime; reDraw();
I min applikasjon blir dette konseptet brukt både i koden som roterer rundt senter og i koden som modulerer bølgebevegelsen. Dette sikrar at applikasjonen verken roterer fryktelig sakte/raskt eller at hastigheita på bølgene er unaturlig på forskjellige maskiner.
Mulige utvidelsar
- Nyttegjere meg av knute-arrayet for å lage spisse bølger.
- Transparent overflate.
- Texture på overflate.
- Betre omgivelsar.

